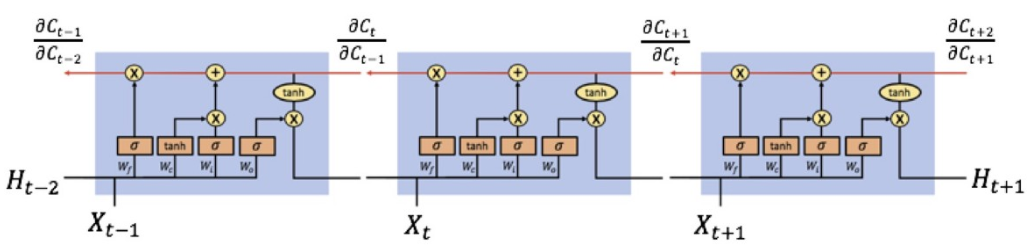
\(c_{t}=c_{t-1} \otimes \sigma\left(W_{f} \cdot\left[H_{t-1}, X_{t}\right]\right) \oplus \tanh \left(W_{c} \cdot\left[H_{t-1}, X_{t}\right]\right) \otimes \sigma\left(W_{i} \cdot\left[H_{t-1}, X_{t}\right]\right)\)

反向传播公式：

\(\begin{aligned} \frac{\partial E_{k}}{\partial W}=& \frac{\partial E_{k}}{\partial H_{k}} \frac{\partial H_{k}}{\partial C_{k}} \frac{\partial C_{k}}{\partial C_{k-1}} \ldots \frac{\partial C_{2}}{\partial C_{1}} \frac{\partial C_{1}}{\partial W}=\\ & \frac{\partial E_{k}}{\partial H_{k}} \frac{\partial H_{k}}{\partial C_{k}}\left(\prod_{t=2}^{k} \frac{\partial C_{t}}{\partial C_{t-1}}\right) \frac{\partial C_{1}}{\partial W} \end{aligned}\)

括号中的部分是累乘项：

$\frac{\partial c_{t}}{\partial c_{t-1}}=\sigma\left(W_{f} \cdot\left[H_{t-1}, X_{t}\right]\right) + $

\(\frac{d}{d \mathcal{C}_{t-1}}\left(\tanh \left(W_{c} \cdot\left[H_{t-1}, X_{t}\right]\right) \otimes \sigma\left(W_{i} \cdot\left[H_{t-1}, X_{t}\right]\right)\right)\)

也就是说，这里的累乘单元是两项和形式，其中前部分是遗忘门的值。遗忘门决定了上一个细胞状态的保留比例，其取值可以接近于1，也就是说可以把遗忘门看成：\(\sigma\left(W_{f} \cdot\left[H_{t-1}, X_{t}\right]\right) \approx \overrightarrow{1}\)，所以LSTM中：

\(\frac{\partial E_{k}}{\partial W} \approx \frac{\partial E_{k}}{\partial H_{k}} \frac{\partial H_{k}}{\partial c_{k}}\left(\Pi_{t=2}^{k} \sigma\left(W_{f} \cdot\left[H_{t-1}, X_{t}\right]\right)\right) \frac{\partial C_{1}}{\partial w} \nrightarrow 0\)

所以，LSTM能缓解梯度消失。